Visual Lens (fluid Window) Visual Lens (Fluid Window),Visual Lens For Compressor,Visual Lens To See Oil Level,Fluid Window To See Oil Level Shenzhen Capitol Micro-Electronics Co.,LTD , https://www.capitolgtms.com
An important analytical method for motor vector control
In the operation of an electric motor, a rotating reference frame that rotates at the same speed as the motor's magnetic field is established. This is commonly referred to as the DQ rotating coordinate system. In this system, all electrical signals can be represented as constant values, simplifying the analysis and control of the motor. The question arises: can the results of the DQ transformation be directly obtained using instruments?
The DQ transformation is a decoupling technique that converts the three-phase windings of an induction motor into an equivalent two-phase winding system. It transforms the rotating reference frame into a stationary orthogonal coordinate system, allowing voltage and current to be expressed in terms of direct current (DC) quantities. This method enables independent control of each variable, effectively reducing the impact of harmonic and unbalanced voltages. Due to the use of synchronous rotation, it becomes easier to separate fundamental wave components from harmonics.
In DC motors, the main magnetic flux is primarily determined by the field current, which is why their mathematical models and control systems are relatively simple. If the physical model of an AC motor could be transformed into a DC-like structure, both analysis and control would become significantly easier. This concept led to the development of coordinate transformations.
Three-phase symmetrical windings A, B, and C, when supplied with balanced sinusoidal currents, produce a rotating magnetomotive force F that moves at the same speed as the current’s frequency. This is illustrated in the figure below.
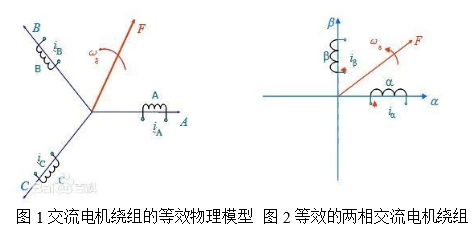
A rotating magnetomotive force does not have to be limited to three-phase systems. Any symmetric multi-phase winding—such as two-phase, four-phase, etc.—can generate a rotating magnetic field when supplied with balanced currents. Two-phase windings, for example, can also create a rotating magnetomotive force if they are driven by currents that are 90 degrees out of phase.
When the magnitude and rotational speed of the magnetomotive forces in different configurations are equal, the systems are considered equivalent. For instance, a two-phase AC winding can be equivalent to a three-phase AC winding. Similarly, a two-phase DC winding, when rotated at the same speed, can replicate the behavior of a static AC winding.
This equivalence allows for the conversion between different coordinate systems. In the DQ transformation, the three-phase AC currents (iA, iB, iC) can be transformed into two-phase stationary currents (iα, iβ) using the Clark transform, and then further converted into a rotating two-phase DC system (id, iq) via the Park transform. This makes it possible to control the motor more efficiently by manipulating these DC-like variables.
### Application of DQ Coordinate Transformation
The theory of coordinate transformation has been widely applied in electrical engineering. It plays a key role in motor control, transient analysis, fault diagnosis, power system stability, and grid quality monitoring. Some of the main applications include:
1. **Motor Control**: Enables precise and efficient control of motor performance.
2. **Transient Analysis**: Helps analyze dynamic behavior during sudden load changes or faults.
3. **Fault Diagnosis**: Assists in identifying and diagnosing motor-related issues.
### Test Methods
DQ transformation is extensively used in motor testing. With accurate rotor position detection and precise measurement of three-phase currents, real-time processing can be achieved using high-speed FPGA technology. The process involves first converting the three-phase stator currents into a two-phase stationary reference frame using the Clark transform, yielding Iα and Iβ. Then, the Park transform is applied to convert the two-phase signal into a rotating reference frame relative to the rotor, resulting in ID and IQ.
The motor control process is essentially the reverse of this transformation. By setting the excitation and torque currents, the system converts them back to the two-phase stationary frame and finally to the three-phase stationary frame, enabling effective motor control.
Currently, ZLG Zhiyuan Electronics is working on integrating DQ transformation into its power analyzers. This will provide valuable insights for motor control design, allowing engineers to compare test results with set values, optimize algorithms, and improve overall performance.
(Source: ZLG Zhiyuan Electronics)